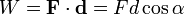Primero tenes que tener en claro que el potencial absoluto se define ARBITRARIAMENTE, como cualquier potencial (gravitatorio o elastico).
Esto quiere decir que si yo tengo una configuracion de cargas, entonces yo puedo elegir cualquier punto del espacio como potencial cero.
Que es precisamente el potencial? Es la energia externa necesaria para llevar una carga positiva de 1 Coulomb desde la posicion elegida como potencial cero hasta dicho punto. Es tambien la energia obtenida del campo electrico en mover la misma carga desde ese punto al punto con potencial cero. Si lo pensas un poco, entonces no importan tanto los potenciales absolutos, sino la diferencia de potencial entre dos puntos.
Ahora, es conveniente a veces elegir el potencial electrico cero en el infinito. Esto se toma cuando la configuracion de cargas es limitada (no hay cargas en el infinito), y genera un campo electrico de la forma K/r^2, es decir que decae con el cuadrado de la distancia: al integrar obtenes un potencial siempre positivo que decae con la distancia: es de la forma K'/r.
La conveniencia se da en las cuentas:
Si tenes un campo electrico de la forma E=K/r^2, entonces el potencial entre a y b sera: Vab = -ʃE*dr (de "b" a "a") = -K'/r (evaluada de "b" a "a") = K'/a - K'/b
siendo Vab = V(a) - V(b)
ahora si vos tomas V(inf) = 0 => Va = Va - V(inf) = Va-inf
Va = -ʃE*dr (de inf a "a") = K'/a - K'/inf = K'/a
porque el termino dividiendo a infinito se hace cero. Entonces para calcular cualquier potencial, ya te libras de hacer integrales, porque el potencial de cualquier punto se calcula como esa K' que obtuviste dividido la distancia del punto al origen.
Asi el potencial absoluto de un punto del espacio esta definido como la energia por unidad de carga necesaria para traer una carga desde el infinito a dicho punto. Tiene esto un sentido intutivo si pensas que en el infinito el campo electrico es cero, pero a medida que te vas acercando aumenta. Asi el potencial es mayor cuanto mas cerca de la carga estas.
Que pasa cuando tenes cargas en el infinito? Por ejemplo cuando tenes un cilindro de longitud infinita, el campo electrico toma la forma K/r, no es mas decayente con el cuadrado de la distancia, sino que decae linealmente. En este caso, cuando integres, el potencial te va a dar una constante multiplicando ln(r). Si vos tratas de evaluar el logaritmo natural en el infinito el resultado te va a dar infinito, y no vas a poder hacer ninguna cuenta. Aca no te queda otra que elegir cualquier otro punto como potencial de referencia. Esto es porque el modelo matematico utilizado es insuficiente o incompleto para abarcar este caso: En electroestatica no se puede tomar potenciales de referencia V=0 en puntos geometricos donde hay carga electrica. Como aca hay cargas en el infinito, no se puede tomar V=0 en ese punto.
miércoles, 16 de mayo de 2012
Video de Trabajo- Fisica
http://www.youtube.com/watch?v=hDyP8WyJGjQ&feature=fvwrel
Muy buen video, me hizo reir es divertido :)
Muy buen video, me hizo reir es divertido :)
Trabajo ( Fisica)
En mecánica clásica el trabajo que realiza una fuerza sobre un cuerpo equivale a la energía necesaria para desplazar este cuerpo. El trabajo es una magnitud física escalar que se representa con la letra 
(del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
Ya que por definición el trabajo es un tránsito de energía, nunca se refiere a él como incremento de trabajo, ni se simboliza como ΔW.
Matemáticamente se expresa como:
es el módulo de la fuerza, 
es el desplazamiento y 
es el ángulo que forman entre sí el vector fuerza y el vector desplazamiento (véase dibujo).
Cuando el vector fuerza es perpendicular al vector desplazamiento del cuerpo sobre el que se aplica, dicha fuerza no realiza trabajo alguno. Asimismo, si no hay desplazamiento, el trabajo también será nulo
(del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.Ya que por definición el trabajo es un tránsito de energía, nunca se refiere a él como incremento de trabajo, ni se simboliza como ΔW.
Matemáticamente se expresa como:
Donde
es el módulo de la fuerza, es el desplazamiento y es el ángulo que forman entre sí el vector fuerza y el vector desplazamiento (véase dibujo).Cuando el vector fuerza es perpendicular al vector desplazamiento del cuerpo sobre el que se aplica, dicha fuerza no realiza trabajo alguno. Asimismo, si no hay desplazamiento, el trabajo también será nulo
Campo Eléctrico
El campo eléctrico es un campo físico que es representado mediante un modelo que describe la interacción entre cuerpos y sistemas con propiedades de naturaleza eléctrica. Matemáticamente se describe como un campo vectorial en el cual una carga eléctrica puntual de valor 
sufre los efectos de una fuerza eléctrica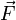 
dada por la siguiente ecuación:
Esta definición general indica que el campo no es directamente medible, sino que lo que es observable es su efecto sobre alguna carga colocada en su seno. La idea de campo eléctrico fue propuesta por Faraday al demostrar el principio de inducción electromagnética en el año 1832.
La unidad del campo eléctrico en el SI es Newton por Culombio (N/C), Voltio por metro (V/m) o, en unidades básicas, kg·m·s−3·A−1 y la ecuación dimensional es MLT-3I-1.
http://www.youtube.com/watch?v=unrN0yulZBg&feature=fvst
sufre los efectos de una fuerza eléctrica 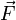dada por la siguiente ecuación:(1)En los modelos relativistas actuales, el campo eléctrico se incorpora, junto con el campo magnético, en campo tensorial cuadridimensional, denominado campo electromagnético Fμν.Los campos eléctricos pueden tener su origen tanto en cargas eléctricas como en campos magnéticos variables. Las primeras descripciones de los fenómenos eléctricos, como la ley de Coulomb, sólo tenían en cuenta las cargas eléctricas, pero las investigaciones de Michael Faraday y los estudios posteriores de James ClerkMaxwell permitieron establecer las leyes completas en las que también se tiene en cuenta la variación del campo magnético.
Esta definición general indica que el campo no es directamente medible, sino que lo que es observable es su efecto sobre alguna carga colocada en su seno. La idea de campo eléctrico fue propuesta por Faraday al demostrar el principio de inducción electromagnética en el año 1832.
La unidad del campo eléctrico en el SI es Newton por Culombio (N/C), Voltio por metro (V/m) o, en unidades básicas, kg·m·s−3·A−1 y la ecuación dimensional es MLT-3I-1.
http://www.youtube.com/watch?v=unrN0yulZBg&feature=fvst
Ley de Columb
Aún cuando los fenómenos electrostáticos fundamentales eran ya
conocidos en la época de Charles Coulomb (1736-1806), no se conocía aún la
proporción en la que esas fuerzas de atracción y repulsión variaban. Fue este
físico francés quien, tras poner a punto un método de medida de fuerzas sensible
a pequeñas magnitudes, lo aplicó al estudio de las interacciones entre pequeñas
esferas dotadas de carga eléctrica. El resultado final de esta investigación
experimental fue la ley que lleva su nombre y que describe las características
de las fuerzas de interacción entre cuerpos cargados.
Cuando se consideran dos cuerpos cargados (supuestos puntuales), la intensidad de las fuerzas atractivas o repulsivas que se ejercen entre sí es directamente proporcional al producto de sus cargas e inversamente proporcional al cuadrado de las distancias que las separa, dependiendo además dicha fuerza de la naturaleza del medio que les rodea.
Como fuerzas de interacción, las fuerzas eléctricas se aplican en los respectivos centros de las cargas y están dirigidas a lo largo de la línea que los une.
La expresión matemática de la ley de Coulomb es:
en donde q y q' corresponden a los valores de las cargas
que interaccionan tomadas con su signo positivo o negativo, r representa la
distancia que las separa supuestas concentradas cada una de ellas en un punto y
K es la constante de proporcionalidad correspondiente que depende del medio en
que se hallen dichas cargas.
El hecho de que las cargas aparezcan con su signo propio en la ecuación anterior da lugar a la existencia de dos posibles signos para la fuerza Fe, lo cual puede ser interpretado como el reflejo de los dos tipos de fuerzas, atractivas y repulsivas, características de la interacción electrostática. Así, cargas con signos iguales darán lugar a fuerzas (repulsivas) de signo positivo, en tanto que cargas con signos diferentes experimentarán fuerzas (atractivas) de signo negativo.
La constante de proporcionalidad K toma en el vacío un valor igual a:
K = 8.9874 · 109 N · m2/C2
esa elevada cifra indica la considerable intensidad de las fuerzas electrostáticas. Pero además se ha comprobado experimentalmente que si las cargas q y q' se sitúan en un medio distinto del aire, la magnitud de las fuerzas de interacción se ve afectada. Así, por ejemplo, en el agua pura la intensidad de la fuerza electrostática entre las mismas cargas, situadas a igual distancia, se reduce en un factor de 1/81 con respecto de la que experimentaría en el vacío. La constante K traduce, por tanto, la influencia del medio.
Finalmente, la variación con el inverso del cuadrado de la distancia indica que pequeños aumentos en la distancia entre las cargas reducen considerablemente la intensidad de la fuerza, o en otros términos, que las fuerzas electrostáticas son muy sensibles a los cambios en la distancia r.
Cuando se consideran dos cuerpos cargados (supuestos puntuales), la intensidad de las fuerzas atractivas o repulsivas que se ejercen entre sí es directamente proporcional al producto de sus cargas e inversamente proporcional al cuadrado de las distancias que las separa, dependiendo además dicha fuerza de la naturaleza del medio que les rodea.
Como fuerzas de interacción, las fuerzas eléctricas se aplican en los respectivos centros de las cargas y están dirigidas a lo largo de la línea que los une.
La expresión matemática de la ley de Coulomb es:
El hecho de que las cargas aparezcan con su signo propio en la ecuación anterior da lugar a la existencia de dos posibles signos para la fuerza Fe, lo cual puede ser interpretado como el reflejo de los dos tipos de fuerzas, atractivas y repulsivas, características de la interacción electrostática. Así, cargas con signos iguales darán lugar a fuerzas (repulsivas) de signo positivo, en tanto que cargas con signos diferentes experimentarán fuerzas (atractivas) de signo negativo.
La constante de proporcionalidad K toma en el vacío un valor igual a:
K = 8.9874 · 109 N · m2/C2
esa elevada cifra indica la considerable intensidad de las fuerzas electrostáticas. Pero además se ha comprobado experimentalmente que si las cargas q y q' se sitúan en un medio distinto del aire, la magnitud de las fuerzas de interacción se ve afectada. Así, por ejemplo, en el agua pura la intensidad de la fuerza electrostática entre las mismas cargas, situadas a igual distancia, se reduce en un factor de 1/81 con respecto de la que experimentaría en el vacío. La constante K traduce, por tanto, la influencia del medio.
Finalmente, la variación con el inverso del cuadrado de la distancia indica que pequeños aumentos en la distancia entre las cargas reducen considerablemente la intensidad de la fuerza, o en otros términos, que las fuerzas electrostáticas son muy sensibles a los cambios en la distancia r.
Suscribirse a:
Comentarios (Atom)